第六章-PN结

• N_A为受主杂质浓度N_D为施主杂质浓度。
• PN结经典工艺：合金法、扩散法。合金结、高表面浓度的浅扩散结：突变结近似。低表面浓度的深扩散结：线性缓变结近似。
• 由载流子浓度引起的扩散运动，与无法移动的电离受、施主构建的空间电荷区引发的漂移运动，达成动态平衡，构建无电压下的平衡PN结。

PN结形成时，电子将从费米能级高的n区流向费米能级低的p区(扩散运动?)而电子的流动导致n区费米能级降低，空穴的运动与之类似，最终，pn两区费米能级归于一致，费米能级的移动是携带能带整体运动的(由于空间电荷区的构建，电子电势在n区不断降低，能带下移，费米能级下移)

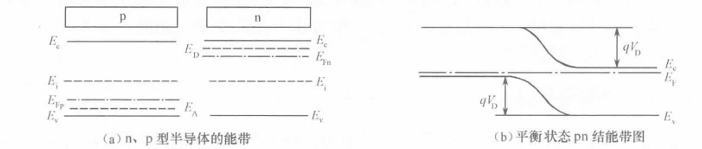
$$ J_n = nq\mu _n\mathscr{E} + qD_n\frac {dn} {dx} $$ 电子从势能低的n区移动到势能高的p区时需要克服势垒，势垒高度刚好补偿PN结费米能级之差。

$$ qV_D=E_{Fn}-E_{Fp} $$ $$ n_{n0}=n_ie^\frac{E_{Fn}-E_i}{k_0T},n_{p0}=n_ie^\frac{E_{Fp}-E_i}{k_0T} $$ $$ n_{n0}\approx N_D,n_{p0}\approx \frac {{n_i}^2} {N_A} $$ $$ V_D=\frac {k_0T}{q}\Big (\ln \frac {N_DN_A}{{n_i}^2}\Big) $$

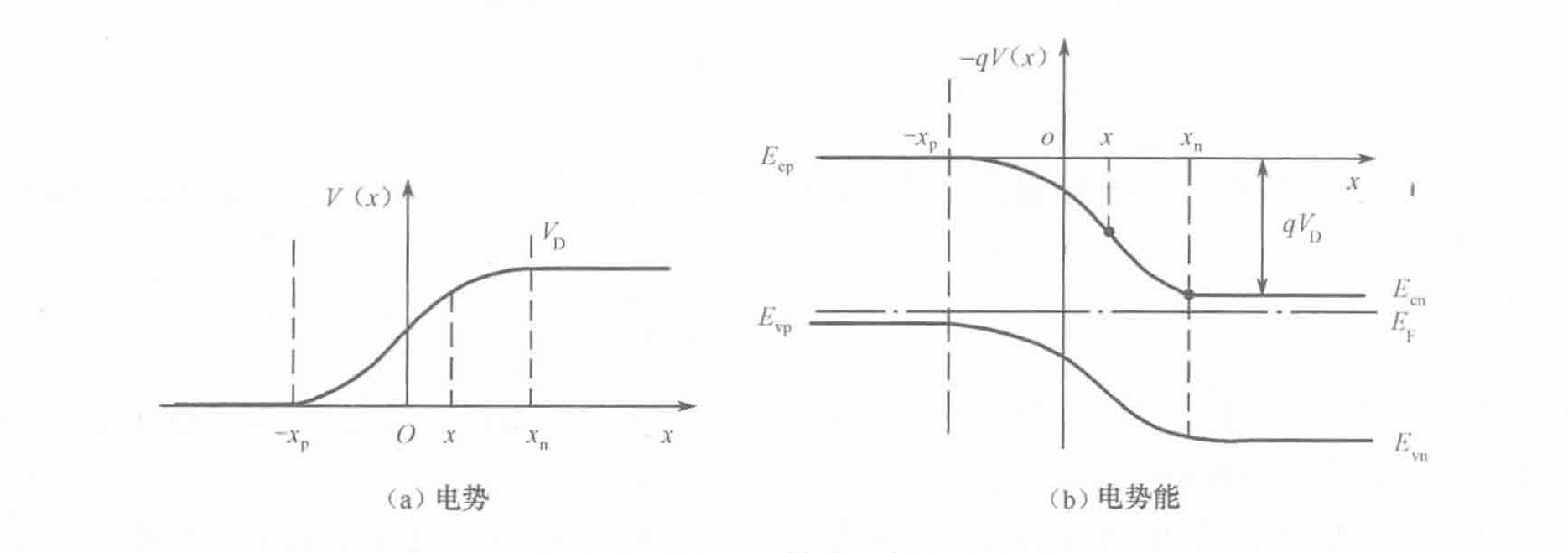
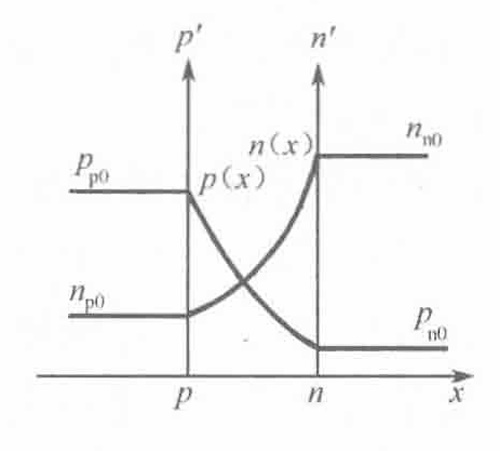
由热平衡状态下的非简并半导体导带电子浓度公式(3-15)可以推出 $$ n(x)=n_{n0}e^\frac{E_{cn}-E(x)}{k_0T}=n_{n0}e^\frac{qV(x)-qV_D}{k_0T} $$ $x=x_n$时$V(x)=V_D$，处于n区，结果为n区平衡多数载流子电子的浓度，而$x=-x_p$时$V(x)=0$，处于p区，结果为p区平衡少数载流子电子的浓度： $$ n_{p0}=n_{n0}e^{-\frac{qV_D}{k_0T}} $$ 同理可得空穴在PN结两端的分布： $$ p(x)=p_{n0}e^\frac{qV_D-qV(x)}{k_0T} $$ $$ p_{n0}=p_{p0}e^{-\frac{qV_D}{k_0T}} $$

P接正正极(外加正向偏压)，电场方向与内建电场相反，空间电荷变少，势垒区变窄，势垒高度变为$qV_D-V$ 总电流等于通过pp’的电子扩散流和通过nn’的空穴扩散流之和。

反向偏压时，总的反向电流等于通过pp’的空穴电流与通过nn’的电子电流之和，由于是少数载流子构成的电流，当反向偏压很大时，边界处的少子可认为是0，因此电流不再随电压变化。

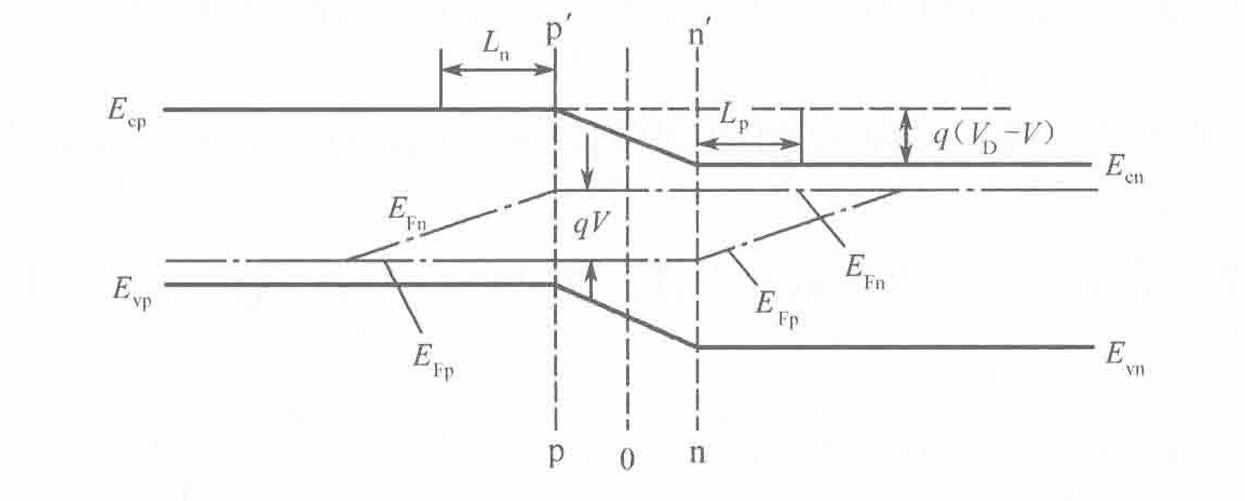
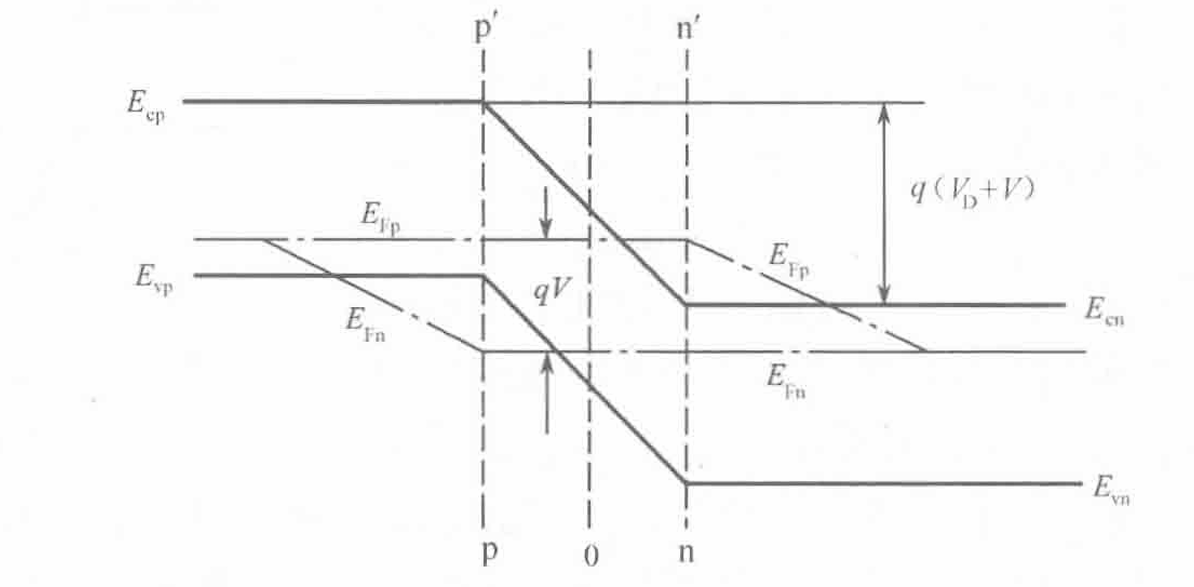
由连续性方程结合$p_n(\infin)=p_{n0}$与$p_n(x_n)=p_{n0}e^\frac{qV}{k_0T}$可以得到非平衡少数载流子在扩散区的分布 $$ p_n(x)-p_{n0}=p_{n0}(e^\frac{qV}{k_0T}-1)e^\frac{x_n-x}{L_p} $$ $$ n_p(x)-n_{p0}=n_{p0}(e^\frac{qV}{k_0T}-1)e^\frac{x_p+x}{L_n} $$

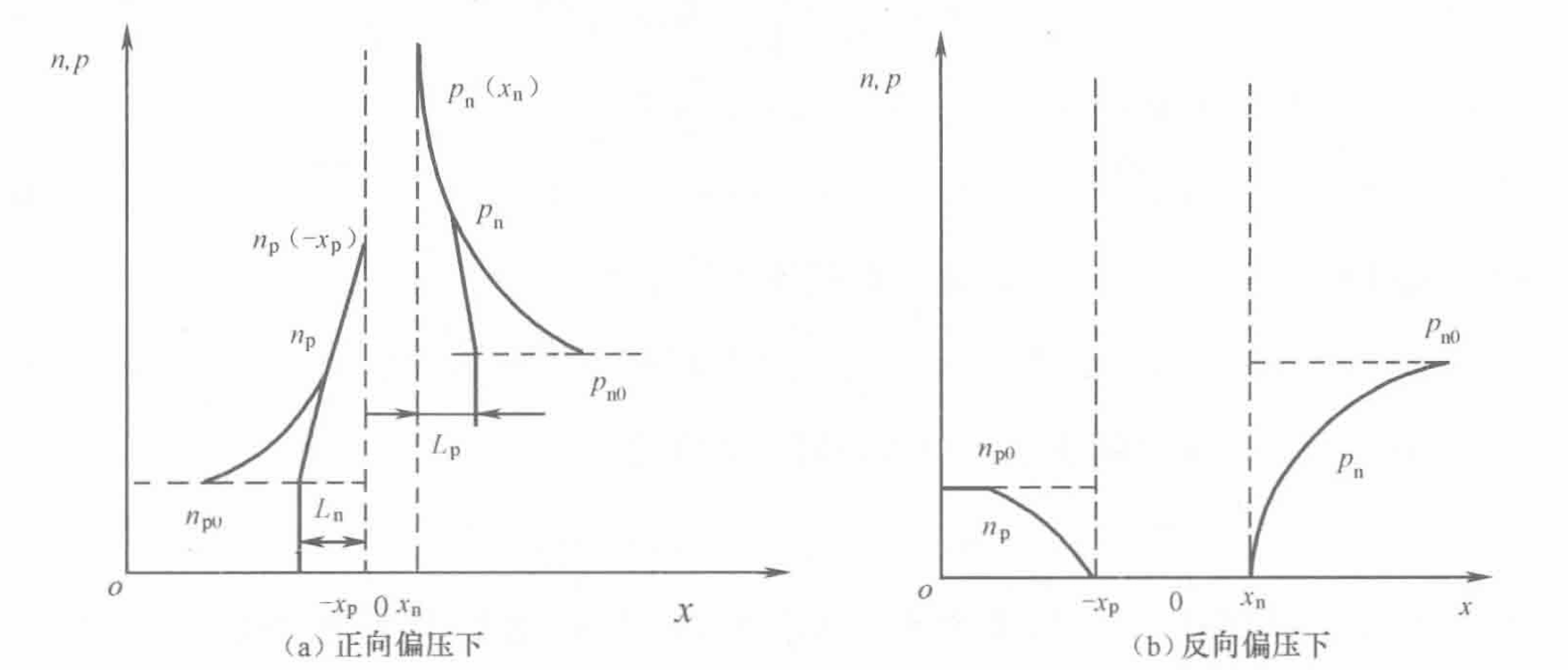
总电流等于p区电子扩散电流与n区空穴扩散电流之和。 $$ J=J_s(e^\frac{qV}{k_0T}-1) $$ 正反向电流密度都随温度升高而增加